1. Abstract
지구상에서 공중에 홀로 떠있는 물체를 제외하면, 어떤 물체던지 항상 다른 물체와 다양한 접촉 상태를 유지하고 있습니다. 이러한 접촉이 일어나고 있는 상태는 움직이지 않는 정적인 상태와 시간에 따라 접촉이 변화하는 동적인 상태 2 가지로 나눌 수 있습니다. 접촉 상태를 유한요소 해석으로 풀기 위해서는 물체의 기하학적인 조건을 고려해야 하는데, 특히 동적인 상태는 물체의 역학적인 움직임마저 같이 분석해야 하는 경우가 많이 발생합니다. 이러한 접촉이 수반된 현상을 분석하는 것을 접촉해석이라고 부릅니다.
2. Technology 배경
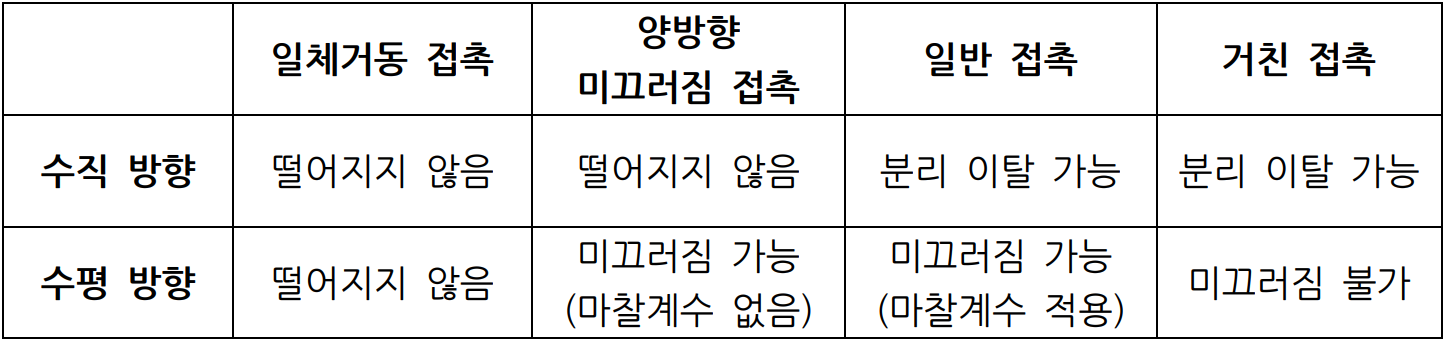
유한요소 해석에서는 접촉을 물리적으로 표현하기 위해서 일반 접촉, 거친 접촉, 일체거동 접촉 그리고 양방향 미끄러짐 접촉 총 4 가지 접촉 조건을 사용합니다. 일반 접촉과 거친 접촉은 물체 간의 동적인 상태, 일체거동 접촉과 양방향 미끄러짐 접촉은 물체의 정적인 상태를 표현하기 위해서 사용합니다. 이러한 접촉을 표현하는 가장 기본적인 원리 중 하나인 벌칙기법과 각 접촉이 어떤 특징을 가지고 있는지 알아보도록 하겠습니다.
2-1. 접촉의 종류
2-1-1. 일체거동 접촉 (선형)
일체거동 접촉은 물체와 물체가 서로 맞닿는 접촉면에 접착체를 바른 것처럼, 독립적인 기하형상의 물체들이 마치 한 몸처럼 움직이는 거동을 표현할 때 사용하는 조건입니다. 이러한 특징 때문에 물체 간의 체결된 현상을 표현하는데 주로 사용되나, 미끄러짐이나접촉면의 마찰 등을 고려할 수는 없습니다.
2-1-2. 양방향 미끄러짐 접촉 (선형)
일체거동 접촉과 동일하게 수직 방향으로 물체가 떨어지진 않으나, 수평 방향으로 미세한 미끄러짐을 표현할 수 있는 접촉입니다. 일체거동 접촉이 표현하지 못하는 미끄러짐을 나타낼 수 있는 특징이 있기 때문에 볼트의 체결 같이 맞닿는 면들이 아주 미세하게 미끄러짐이 일어나는 현상을 파악할 수 있습니다.
2-1-3. 일반 접촉 (비선형)
일반 접촉은 우리가 물리적으로 알고 있는 접촉이란 개념에 가장 가까운 접촉 조건이며, 동시에 많은 기계적 현상을 표현하기 위해서 많이 사용하게 되는 조건입니다. 물체의 미끄러짐을 표현할 수 있으며, 이때 마찰계수까지 고려 할 수 있습니다. 그리고 기하학적 조건에 따라 수직 방향으로 물체 간의 접촉이 떨어지는 것을 표현할 수 있습니다.
2-1-4. 거친 접촉 (비선형)
일반접촉과 동일하게 수직 방향으로 물체의 접촉이 끊어질 수 있으나, 수평 방향으로의미끄러짐은 고려하지 못하는 접촉 조건입니다. 물체와 물체 간의 맞닿는 면이 매우 거칠어 미끄러지지 않을 때에 사용하는 접촉으로서 일반접촉보다 좀 더 특수한 경우에 사용되는 접촉입니다.
2-2. 접촉의 선형성과 비선형성
일체거동과 미끄러짐 접촉은 해석 초기 위치에 따라 접촉 조건이 부여되어 항상 일정한 선형성을 가지고 있습니다. 반면 일반접촉은 하중과 모델의 형상에 따라 변형이 발생하게 될 때 접촉이 일어나는 위치가 변화하게 되며, 이때 전체 모델을 해석하기 위해 만든 방정식이 비선형적으로 변화하게 됩니다. 동시에 접촉 위치에서 발생하는 접촉력이 요소의 침투량에 따라 선형적으로 증가하지 않고 급격히 커지게 됩니다.
즉 접촉 상태가 바뀔 때 마다 모델을 구성하고 있는 여러 조건이 비선형적으로 바뀌게 되므로, 물체의 동적인 상태를 표현할 수 있는 일반 접촉과 거친 접촉은 비선형해석에서만 사용할 수 있습니다.
2-3. 벌칙 기법
벌칙 기법은 구속조건 등을 수치적으로 처리하는데 있어 정확도를 조금 낮추어 수렴성과 해석 시간을 단축시키는 방법 중 하나 입니다. 이 기법은 일반적으로 구속조건을 스프링이 대체하는 예제로 설명됩니다.
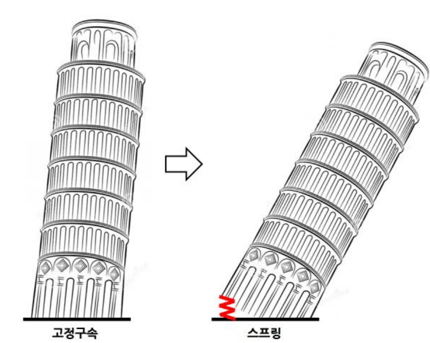
피사의 사탑에 이 벌칙기법을 적용한 예를 들어 보겠습니다. 피사의 사탑은 기울어져 있으나 단단한 지반이 이를 지지하여 무너지지 않도록 버티고 있습니다. 이 단단한 지반 대신 어떤 스프링이 피사의 사탑을 지지하고 있다고 생각하면 어떨까요?지반을 대신한 스프링의 강성이 약하면 약할수록 지면과 피사의 사탑 하부가 점차 벌어지게 되고, 그만큼 피사의 사탑은 기울어지게 될 것입니다.
반대로 스프링의 강성이 점차 강해질수록 스프링이 피사의 사탑 하부를 단단히 지지하게 될 것이며, 피사의 사탑하부와 지면의 거리가 0 에 가까워지면서 실제 지반이 지지하는 현상과 동일하게 될 것입니다. 이렇듯 벌칙 기법을 이용하면 단순히 스프링의 강성을 조절하는 것 만으로 구속조건, 접촉 등 여러 물리 현상을 수치해석적으로 표현하여 사용할 수 있습니다.
2-4. 벌칙 기법과 비선형 접촉
유한요소해석에서는 물리적인 접촉을 표현하는 여러가지 방법이 있으나, 그 중 가장 많이 사용하는 기법은 벌칙 기법입니다. 벌칙기법은 기하학적 거동에 따라 요소망의 접촉이 발생하게 되면 먼저 접촉을 묘사하지 않고, 요소망 사이에 미세한 침투가 발생하도록 합니다. 그 뒤 미세한 침투가 발생한 요소면에 침투량만큼의 길이를 가지는 벌칙 강성, 즉 스프링을 침투한 요소면 사이에 생성합니다.
요소면 사이에 생성된 스프링은 스프링 강성에 따라 침투되어 있는 요소망이 바깥으로밀려나가도록 힘을 가하게 되며, 이에 따라 침투량이 0 에 가까워질수록 실제 접촉이 일어난 것과 동일한 현상을 표현하게 됩니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
