1. Abstract
1 차원 유동 네트워크 모델링은 단면의 형상이 단순하여 1 차원 요소를 이용한 모델링으로 간략화 할 수 있는 채널(Channel)을 포함한 시스템의 유동 특성을 계산하기 위해 사용합니다. 특히 단면 형상의 규모에 비해 길이가 긴 관(Pipe) 내부 유동의 경우 완전히 발달된 유동 특성은 단면에 따라 일정하고 단순함에도 불구하고 3 차원 관으로 모델링하여 해석을 수행하면 필요 이상으로 많은 수의 요소망을 필요로 하게 되며, 결과적으로 과도한 계산 비용이 초래됩니다.
midas NFX CFD 의 1 차원 유동 네트워크 모델링 기능을 이용하면 2 점 및 다절점 조건을 통해 분절된 채널 유동을 계산할 수 있을뿐 아니라, 채널 표면의 열교환 및 3 차원 요소망과의 커플링 계산을 수행할 수 있습니다.
- 2. Technology 배경
2-1. 1차원 유동 네트워크 기능
많은 분절점(Junction)을 포함하고 있는 배관 시스템에 대해서, 각 분절점에 분배되는 유량비 및 관내 유압, 혹은 필요할 경우 각 지점의 유체 온도를 계산하기 위해 유동 해석을 필요로 하는 경우가 있습니다. 특히 플랜트 배관 시스템의 경우 그 규모가 상당하고 관 및 분절점의 개수가 많아서(그림 1), 이를 3 차원 유동 해석으로 진행하는 데에 몇 가지 어려움이 따르게 됩니다. 많은 수의 요소망을 필요로 함으로서 과도한 계산 비용이 초래되며, 모델의 규모에 비해 관내 유동의 유선 길이가 길어지게 되어 해석의 수렴성에도 좋지 않은 영향을 줄 수 있습니다.
단면의 형상이 단순하고 그 규모에 비해 길이가 긴 관의 내부 유동은 얼마 지나지 않아 완전 발달(Fully developed)되며, 모든 유동 변수는 단순히 길이의 함수로서 표현이 가능합니다. 완전 발달 유동의 경우 이미 연구된 다수의 결과들이 존재하여 관내 유체 현상을 단순화하는 데 도움을 줄 수 있습니다.
분절점의 형상이나 확관 및 축관, 심지어는 관의 재질마저도 어느 정도 정형화가 가능하여, 이에 따라 많지 않은 케이스로 거의 모든 배관 시스템을 표현하는 것이 가능하며, 이를 이용하면 시스템을 표현하고 이에 따라 설계된 단순한 1 차원 유동 방정식을 해석하는 것이 가능합니다. 또한 사용자들은 같은 단면의 서로 다른 위치에서의 물리량 차이보다, 길이에 따른 물리량의 차이를 알고자 하는 경우가 많습니다.
그림 1 화공 플랜트의 배관 시스템
midas NFX CFD 에서는 2 절점 및 다절점 경계조건 기능을 이용하여 1 차원 요소에 대한 연결 정보를 입력할 수 있으며 열해석도 수행할 수 있습니다.1 차원 유동 네트워크 기능은 플랜트 뿐 아니라 얇고 긴 배관을 포함한 많은 시스템에 대해 효율적인 계산을 가능하게 합니다. midas NFX CFD 에서는 기본적으로 제공되는 네트워크 시스템의 해석 뿐 아니라, 1 차원과 3 차원 요소의 커플링 기능을 지원합니다. 이를 이용하면 챔버와 관이 연결된 시스템의 해석이 가능합니다. 또한, 유체 및 고체에 삽입된 배관 시스템의 열교환 해석 역시 가능합니다. (그림 2)
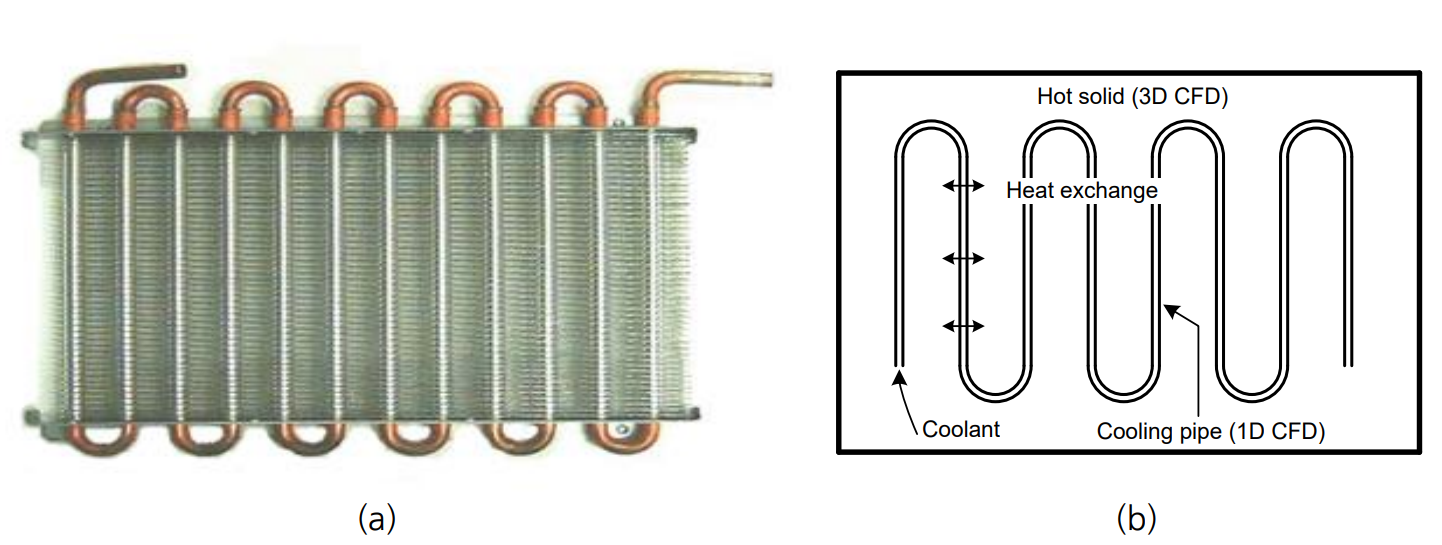
그림 2 (a)실제 열 교환기의 형상과 (b)1D 모델링 형상
이 밖에도 단순 확관 및 축관 해석 기능을 이용한 CDV 노즐 해석 뿐 아니라, 샤워 헤드, 복잡한 챔버 시스템의 해석이 1 차원 유동 네트워크 기능을 통해 가능합니다.
2-2. 부손실 계수
관 유동에서 유체에 적용되는 벽면 마찰력은 유체 거동을 계산하는 과정에서 중요한 변수로 작용합니다. 이 중 형상이 변하는 지점에서 생기는 손실 계수를 부손실 계수(minor loss coefficient)라고 하는데, 이 값은 형상에 따라 어느 정도 알려진 값을 사용합니다. 대표적인 급변 형상에 대한 부손실 계수 KL을 그림 3 에 나타내었습니다. 연결부 형상에 따라 부손실 계수를 최대 두 개로 나타내었습니다.
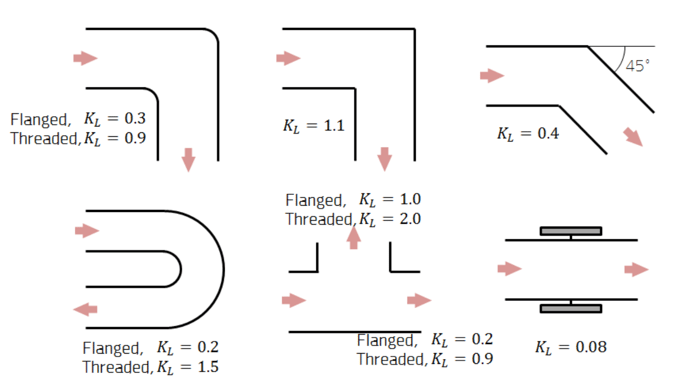
그림 3 대표적인 관 연결부의 부손실 계수
3. Technology 이론 소개
3-1. 지배 방정
1차원 파이프 또는 채널 유동은 Navier-Stokes 방정식에 단면적을 고려한 형태, 즉 질량 보존 또는 연속 방정식과 운동량 보존식을 따릅니다. 질량 보존 방정식은 다음과 같습니다.
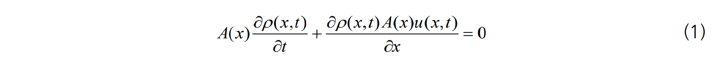
A (x): 단면적
u (x, t) : 속도
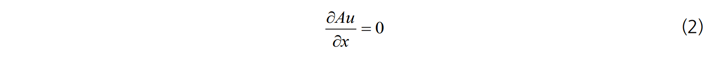
운동량 보존식 역시 단면적 A를 이용하여 간단하게 정리할 수 있으나, 유체의 점성에 의한 효과는 경험적인 벽면 마찰력을 통하여 고려합니다.
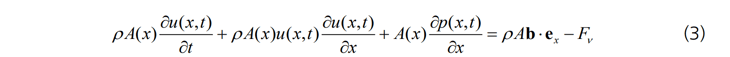
b: 단위 질량당 체적력(body force)
ex: 요소의 방향을 나타내는 단위벡터
Fv: 유체의 점성에 의한 벽면 마찰력
벽면 마찰력은 동압력(dynamic pressure)과 Darcy-Weisbach 마찰인자(friction factor)에 비례한다고 가정하여 다음과 같이 나타낼 수 있습니다.
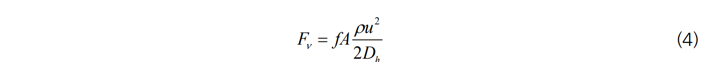
f: Darcy-Weisbach 마찰인자
Dh: 수력학적 직경(hydraulic diameter)
유동의 속도가 느린 층류의 경우 마찰인자 f는 층류 형상계수(shape coefficient)와 Reynolds 수에 의해 결정된다고 알려져 있으며 다음과 같습니다.
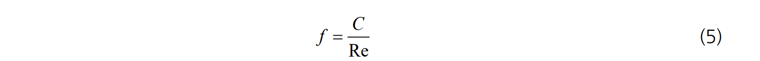
파이프 또는 채널 유동의 Reynolds 수는 아래와 같이 정의할 수 있습니다.
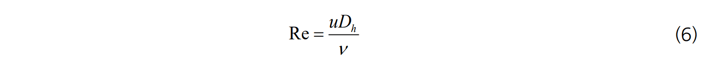
난류 유동의 경우에는 Reynolds 수와 표면 조도 높이(surface roughness height)에 의해 마찰인자 f가 결정되며, 실험적 데이터에 근거한 Colebrook 공식을 이용합니다.
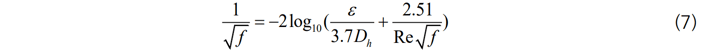
midas NFX CFD 에서는Re > 2300 인 영역에 대해 난류 유동으로 판단하여 식 (7)을 적용하지만, 일반적으로 2000 < Re < 4000 의 경우에는 천이영역으로 알려져 있으며, 마찰인자를 결정하는 방법이 정립되어 있지 않습니다. 열전달 지배 방정식은 단면적을 고려했을경우 다음과 같이 정리할 수 있습니다. 아래의 식에서 유체의 점성에 의한 에너지 소산항은 생략하였습니다.
😥 미리 보기는 여기까지!
내용을 이어서 보고 싶다면,
아래 정보를 입력해 주세요.
